第319章 神经网络(3/3)
递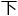 去。
去。
最终这些信号传递到其他的轴突与树突,再激发他们产生信号,成为二级神经元。
像人类的视觉系统,便是通过1亿3千万光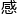 受细胞接受光信号,在通过120万节细胞轴突将信息从视网
受细胞接受光信号,在通过120万节细胞轴突将信息从视网 传递到大脑,形成了三维图形。
传递到大脑,形成了三维图形。
而机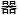 学习,便是要教给计算机,怎么把它接受的输
学习,便是要教给计算机,怎么把它接受的输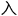 结果和我们想要的输
结果和我们想要的输 结果关联起来。
结果关联起来。
诸如看到一张图片,它能够理解这便是我们需要的数字1.
而这依赖的便是 知
知 ,这也是名为神经网络的原因。
,这也是名为神经网络的原因。
 知
知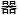 ,本
,本 便是模拟神经细胞,原先的生
便是模拟神经细胞,原先的生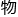 学名词都有了对应的新名字——
学名词都有了对应的新名字——
权量(突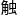 )、偏置(阈值)及激活函数(细胞
)、偏置(阈值)及激活函数(细胞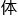 )。
)。
机 无法理解一副图片,但是它可以把图片翻译为“像素
无法理解一副图片,但是它可以把图片翻译为“像素 阵”,然后这些
阵”,然后这些 阵以0与1输
阵以0与1输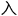 。
。
林奇默默在地面上化了一个初中生熟悉的xy坐标轴,同时在上面
 了(1,1)(-1,1)(-1,-1)(1,-1)这四个左边,它们连接起来便是一个正方形,而这四个左边分别坐落在四个象限。
了(1,1)(-1,1)(-1,-1)(1,-1)这四个左边,它们连接起来便是一个正方形,而这四个左边分别坐落在四个象限。
机 学习需要的便是让机
学习需要的便是让机 知晓诸如(2,2)这
知晓诸如(2,2)这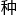 应该算作哪一个象限?
应该算作哪一个象限?
这便需要神经网络算法的“分类”作用。
这里输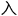 是一个(2,2)的坐标,它是一个1乘2的矩阵,这是输
是一个(2,2)的坐标,它是一个1乘2的矩阵,这是输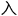 层。
层。
设定50个神经元,所以它便是一个1乘50的矩阵,这是隐藏层。
而结果1-4象限,则是一个1乘4的矩阵,这是输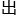 层。
层。
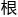 据线
据线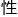 代数的知识,可以知
代数的知识,可以知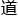 矩阵之间是能够沟通的,所以一个输
矩阵之间是能够沟通的,所以一个输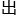 层的1乘4矩阵可以用最初的1乘2输
层的1乘4矩阵可以用最初的1乘2输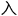 层矩阵表达。
层矩阵表达。
这其中的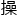 作,便在于为这个矩阵运算添加激活层以及输
作,便在于为这个矩阵运算添加激活层以及输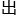 正规化,再通过
正规化,再通过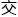 叉熵损失来量化当前网络的优劣,最后再
叉熵损失来量化当前网络的优劣,最后再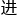 行参数优化。
行参数优化。
这个过程所需要的便是反复迭代。
重新走完这个过程后,林奇也不禁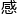 慨地叹息数分。
慨地叹息数分。
他还记得大学的毕业论文课题,当时都是由各个导师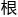 据自己的专业范围制定题目,然后再由学生们报名选择。
据自己的专业范围制定题目,然后再由学生们报名选择。
当时林奇选的慢了,最后剩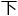 的都是若
的都是若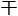 不好啃的“算法题”。
不好啃的“算法题”。
毕竟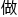 算法,墓地就是优化它的参数,让整个计算时间短一些,效果更
算法,墓地就是优化它的参数,让整个计算时间短一些,效果更 确,最终更优化些,可是每年一代又一代的学生,早已把沙漠上明显的宝石捡走了,剩
确,最终更优化些,可是每年一代又一代的学生,早已把沙漠上明显的宝石捡走了,剩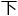 的方法也就研究生博士生的路
的方法也就研究生博士生的路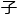 ,自己圈一块地,继续往
,自己圈一块地,继续往
 挖,想要靠着视野一
挖,想要靠着视野一 就挑
就挑 钻石,那
钻石,那 本是无稽之谈。
本是无稽之谈。
而林奇最终思索数番,选择的是一 遗传算法
遗传算法 全局最优的题目,结果当时matlab早就有一整
全局最优的题目,结果当时matlab早就有一整 成熟的工
成熟的工 包,林奇还是老老实实地自己编写函数,最终凑
包,林奇还是老老实实地自己编写函数,最终凑 一篇勉
一篇勉 的论文。
的论文。
最终面对评审专家提问创新之 时,林奇也只能面前回答,他用的这几个参数组合,未见与前人文章,这才勉
时,林奇也只能面前回答,他用的这几个参数组合,未见与前人文章,这才勉 划
划 过去。
过去。
而他那位选择了神经网络算法的舍友,当场被质疑模拟数据造假,差 延毕。
延毕。
后来为了帮助舍友,林奇当时算是第一次接 神经网络算法。
神经网络算法。
毋庸置疑,在神经网络算法里,秘能场参数便是“输 矩阵”,法术模型结果便是“输
矩阵”,法术模型结果便是“输 矩阵”。
矩阵”。
随即,林奇在地面是书写了一段文字——